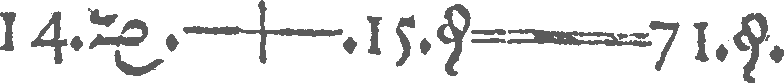Math FoundationsEquations

Elementary Equations

Learn how to solve and transform elementary equations step by step. Simple and visual, with clear examples and without memorizing a bunch of obscure rules. This is a key foundational skill in mathematics and the exact sciences.
Key elements:
Connections:
Statistics:
Term3
Statement1
Important4
Problem36
ArticleSummaryPractice

This is basics!

The skill of transforming equalities and solving equations is fundamental to all mathematics and exact sciences. Try to solve as many problems as possible. Regardless of whether you managed to solve the problem or not, always open the solution and check the correctness of your reasoning.

Don't rush!

If you have no experience in solving equations, do not rush to do as much as possible at once. Spread the practice problems over several days. A day for “basics” level problems, a day for “normal”, a day for “advanced”. At the beginning of a new day, re-solve the problems you had difficulties with the previous time.

Simple equations

😀
Elementary
Solve the equation:
x+100=1x + 100 = 1

First printed equation

😀
Elementary
You have the honor of solving the first printed equation in history!
In modern notation:
14x+15=7114x + 15 = 71

War axe

Elegant
😀
Elementary
An axe weighs a kilogram and a half of an axe.
How much does the axe weigh?

He multiplied by zero…

😀
Elementary
Matvey is solving the equation x + 3 = 5. He was too lazy to think, so he decided to pull a fast one. He said that the solution to the equation is the number 10.
To justify his solution, he substituted 10 instead of x into the equation, and then multiplied both sides of the equation by 0:
10+3=5⋅0 ∣ 10+3=5 ∣ ⋅0(10+3)⋅0=5⋅00=010 + 3 = 5 \\ \brand{\cdot 0} \ | \ 10 + 3 = 5 \ | \ \brand{\cdot 0} \\ (10 + 3) \cdot 0 = 5 \cdot 0 \\ 0 = 0
Since the result is a true equality, then 10 is the solution to the equation x + 3 = 5. Today, you are thinking for Matvey. Is he right? If not, explain specifically what is wrong with his solution.

Cats vs… Trees

😀
Elementary
Find the height of the cat.

Some number

😀
Elementary
Some number was multiplied by 2, then 10 was added and 100 was obtained. What was that number?

Price with a trick

Elegant
😀
Elementary
A baseball bat and a ball together cost 110 rubles. The bat costs 100 rubles more than the ball. How much does the ball cost?
First try to solve the problem quickly in your head. Then solve it using an equation and compare the results.

Concrete mixer mixing concrete

Applied
😀
Elementary
You are going to build your own house! For this you need a lot of concrete. Concrete is formed by mixing cement and sand in a ratio of 1:3, that is, for one kilogram of cement you need three kilograms of sand. How much cement and sand do you need if you want to mix 100 kg of concrete?

Idiot's Triangle

😀
Elementary
Magic triangle of electric power:
Original equality:
P=I2RP = I^2 R
Derive equalities for I2I^2 and R.

Growing up

😀
Elementary
Vanya is 2 times older than Liza. If you add their ages together, you get the number 24. How old are Vanya and Liza?

Fathers and sons

Elegant
😀
Elementary
When I was 14, my father was three times older than me. He is now twice as old as me. How old am I?

Medium equations

🤔
Intermediate
Solve the equation:
x2−121=0x^2 - 121 = 0

Linear equations formula

🤔
Intermediate
Derive a general formula for solving any linear equation of the form:
Ax+B=0,A≠0Ax + B = 0, \enspace A \neq 0

Twist and turn, to confuse I want

Method
Elegant
🤔
Intermediate
Imagine that you have the following equality:
ax2+bx+c=y3−tax^2 + bx + c = y^3 - t
Now let's take and simply swap the left and right sides of the equality:
y3−t=ax2+bx+cy^3 - t = ax^2 + bx + c
  1. 1
    Strictly prove that any equality can be reversed and it will remain true.
  2. 2
    Strictly prove that any equality can be reversed using the same action rule.

Big Journey

🤔
Intermediate
Alina went on a 3 day hike. The length of the entire route was 111 kilometers. On the second day she covered 5 kilometers more than on the first. And on the third day she covered 10 kilometers less than on the second. How many kilometers did Alina cover every day?

Zero Factors

Method
🤔
Intermediate
As a result of transformations, equations are often reduced to a product of factors on one side and zero on the other. Such equations are solved very simply, and now you will learn how to do it. Let's start with an elementary example:
(x+3)(x−2)=0(x + 3)(x - 2) = 0

Flipping Fractions

Method
🤔
Intermediate
Speaking of non-standard actions on equalities, students often like to use the so-called “fraction flipping”. This action consists of swapping the numerator and denominator of fractions on the left and right sides of the “equals” sign. For example:
3x+2=24⇒x+23=42\frac{3}{x+2} = \frac{2}{4} \quad \Rightarrow \quad \frac{x+2}{3} = \frac{4}{2}
Solve this equation to the end and verify by substitution that the obtained root is indeed correct.

Mystery of Flipping Fractions

🤔
Intermediate
To solve the equation, Tanya decided to use the fraction flipping technique:
1x+13=28⇒x+3=82\frac{1}{x} + \frac{1}{3} = \frac{2}{8} \quad \Rightarrow \quad x + 3 = \frac{8}{2}
Did she do the right thing? If not, explain in detail what went wrong and solve the equation correctly.

Complete Opposite

🤔
Intermediate
For what value of p will the expressions 3p – 1 and 5(p + 5) be opposite numbers? Find these opposite numbers.

You'll Never Guess!

🤯
Advanced
Solve the equation in the article that was used as an example of an equation that cannot be solved by guessing:
x+743 63928−18x=2025x\frac{x + 743 \ 639}{28} - 18x = 2025x

Think 7 times, act once

Method
🤯
Advanced
Among the suggested actions, choose the one that allows solving the equation in fewer steps. Explain in detail why the chosen action is better compared to the other.
If you don't know which action to choose, solve the equation twice using both actions, and then it will become clear which action was more effective.
3x+2=x3x + 2 = x
Actions:
  1. 1
    Group x on the left side of the equation.
  2. 2
    Group x on the right side of the equation.

Advanced Equations

🤯
Advanced
Solve the equation:
−4x2+2x+6=−2x2+3x−(−3+2x2)-4x^2 + 2x + 6 = -2x^2 + 3x -(-3 + 2x^2)

Fractional Commotion

🤯
Advanced
Solve the equation:
3z+96+8z−24=5+4z3\frac{3z + 9}{6} + \frac{8z - 2}{4} = \frac{5 + 4z}{3}

Preservation of Equality Falsity

🤯
Advanced
The same action rule is about true equalities. But does it apply to false equalities? Is it true that if the same action is performed on both sides of any false equality, the result will necessarily be a false equality?

Linear Root Classes

Elegant
🤯
Advanced
The three equations below have the form Ax + B = 0 (they are called linear) and differ from each other only by a constant factor. They all have one common root −32-\frac32:
2x+3=0Original\underset{\text{Original}}{2x + 3 = 0}
4x+6=0Multiplied by 2 \underset{\text{Multiplied by } 2}{4x + 6 = 0}
6x+9=0Multiplied by 3 \underset{\text{Multiplied by } 3}{6x + 9 = 0}
Dividing both sides of the second equation by 2, and the third by 3, we will again get the original first equation. Multiplying both sides of the second equation by 32\frac32, we will get the third equation. In short, all three equations can be transformed into each other by multiplying by some number.
Are there two equations with identical roots that cannot be transformed into each other by multiplying by some number? If they exist, give an example of such equations. If they do not exist, strictly prove it.

Logic of Solving Equations

Up to this point, we have solved equations quite loosely. We found solutions and implicitly assumed that there were no other solutions. We treated equations with no solutions and with an infinite number of solutions just as loosely.
It is absolutely normal and intuitively understandable to solve this way. But if you really want to dig a little deeper and provide a strict and clear logical justification for the solution of equations, then solve the following problems. Or at least read their solutions.

No Solutions

Elegant
🤯
Advanced
When, as a result of transformations, we arrive at a false equality with no variable at all, we say that “the equation has no solutions”. But if we arrived at a false equality, on what basis do we consider that the original equation has no solutions? After all, its truth value is not established, and for false equalities the rule of the same action does not work!
For example, the equation x + 3 = x – 2 as a result of subtracting x from both sides of the equation was reduced to the false equality 3 = –2. Logically explain why the thesis “we got the false equality 3 = –2” implies that “the equation x + 3 = x – 2 has no solutions”.

Finite Number of Solutions

🤯
Advanced
By definition, “to solve an equation is to find its roots and prove that there are no others”. When we, for example, by subtracting 5 from both sides of the equation x + 5 = 10 arrive at an equality like x = 5, we say that we solved the equation and found its only solution 5. Does this prove that the equation has only one solution? What if there are some other roots?
Is solving an equation by means of transformations according to the rule of the same action a proof that the equation has no other roots?

Infinitely Many Solutions

🤯
Advanced
When, as a result of transformations, we arrive at a true equality with no variable at all, can we say that it has “infinitely many solutions”? That “any number will be its root”?
For example, the equation x + 3 = x + 3 as a result of subtracting x from both sides of the equation was reduced to the true equality 3 = 3. Can we say that from the thesis “we got the true equality 3 = 3” it follows that “the equation x + 3 = x + 3 has infinitely many solutions”?
Elementary Equations