Elementary Equations
Key elements:
Connections:
Statistics:
Term3
Statement1
Important4
Problem36
Why so many words?
It might seem like a primitive topic! What could be simpler than elementary equations? There really is nothing complicated about them. However, for some reason, it always turns out that analyzing the simplest questions requires the most thorough explanations. This is because it is the base and foundation, which is critically important to understand correctly.
That is why everything is described here so that you 100% understand the basic principles of working with equalities and equations. This ensures that those basic actions do not limit you with any contradictions or misunderstandings. So that, if necessary, you could explain every step of solving any equation in detail yourself.
Literally you after reading this article
The article might seem too large for such a simple topic, but don't worry — there is nothing complicated here. Most of the text is taken up by various examples ensuring that you understand everything correctly and will not make typical mistakes.
Equality
Let's look at the word “equation” more closely. It is related to “equal”, “to equate”, that is, to make equal, to make an equality. Interesting word… Before talking about equations, let's first figure out what “equality” is!
In mathematics, we can write the same abstract object in different ways. For example, the number 3 can be written in an infinite number of different ways:
- 3
- 1 + 2
- 1 + 1 + 1
- 5 – 2
- and so on…
The notations are different, but they all denote the same abstract object — “number three”. To show that different notations denote the same object, mathematics uses the equals sign =.
Now that we understand the purpose of the equals sign, we can formulate the definition of equality in mathematics:
Equality
Two expressions with an equals sign (=) between them.
Not only numbers can stand on the sides of the equals sign, but also more complex constructions. Even the already mentioned number 3 can be written as a single digit “3” or as a complex construction like “1 + 1 + 1”. Sometimes letters denoting some unknown numbers can stand there. To avoid clarifying every time what exactly should stand on the sides of the equality sign (numbers, letters, additions, multiplications, functions, …), all this together is called by the general word expression. Therefore, the definition of equality refers specifically to “expressions”.
There are no restrictions on what can stand on the sides of the equals sign. You can write anything you want there. Therefore, equalities are divided into two categories: true and false.
- 1True equality is an equality in which expressions to the left and right of the equals sign denote the same object.
- 2False equality is an equality in which expressions to the left and right of the equals sign denote different objects.
Equalities in Real Life
Like many other mathematical concepts, equality has analogies in real life. And very visual and accurate ones, which you have definitely encountered.
On a playground, you can almost always find a seesaw — a construction consisting of a long board lying on a support in the middle. If children of the same weight sit on both sides, the seesaw is in balance and does not tilt to either side. This is an example of true equality.
True equality can also be obtained in a more interesting way: for example, an adult can sit on one side, and a couple of children on the other. Then to the left of the “equals sign” will be the weight of one adult, and to the right — the sum of the weights of two children.
True equality

Equality 5 = 2 + x
Weight of the unknown weight is 3
A more convenient analogy is mechanical scales. In essence, this is the same seesaw, but only more precise and intended not for fun, but for weighing all sorts of objects in different quantities. There are also special weights. The weight of some weights is known (these are ordinary numbers in equalities), and others are not (these are unknowns: a, b or x).
The analogy with mechanical scales will be very useful to us later, remember it. It not only illustrates the concept of equality well, but also helps to visualize its transformations.
Equation
Now that we have dealt with the concept of equality, we can move on to equations. Everything is quite simple here. Sometimes, an unknown number is present in an equality. This unknown number can be designated, for example, with a question mark:
It is easy to guess what numbers are hidden behind the question marks: 3, 5, 2 and 32. In mathematics, it is customary to denote unknown numbers by letters, for example, x, y, z and so on. It is more convenient to write equations with several unknowns this way, and you can show which unknowns are equal to each other. Compare for yourself:
On the left, you can't tell what is what. But on the right, it is clearly understood that there are only two unknowns (x and y), and not four as it might seem from the left equality. And if we find, for example, x, then we can immediately substitute it in two places!
Equation
Equality in which there is one or more unknowns or variables.


The First Printed Equation
The first printed appearance of the equals sign, and at the same time the equation in a “quasi-modern” form, occurred in 1557 in the book “The Whetstone of Witte” by the English mathematician and physician Robert Recorde. He introduced the equals sign itself to, quote “avoide the tediouse repetition of these woordes: is equalle to”. And the equation looked like this:
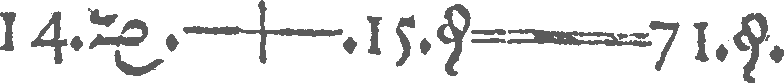
Looks scarce, but quite readable.
And here is the same equation in modern notation:
And here is the same equation in modern notation:
Solving an Equation
We realized that any equation is just an equality with unknowns. Recall that an equality can be true or false. By substituting some numbers into the equation instead of unknowns, we can obtain both true and false equalities. Consider this equation:
Substituting the number 1 instead of x, we will get a true equality. And if we substitute any other number, for example 2, then we will get a false equality:
That is, we literally “equate” the equality, balance abstract scales in search of equilibrium, look for values at which the left side will be equal to the right. At x = 1 the scales are balanced, and at x = 2 the left bowl of the scale is heavier than the right one and they tilt to the left.
Solving an Equation
Solutions or roots of an equation are numbers that, when substituted for unknowns, turn it into a true equality.
“To solve an equation” means to find all its roots and prove that there are no other roots. Moreover, there may be no roots at all, or there may be infinitely many.
To solve the simplest equations, you don't even need to know any rules and methods. You can simply guess the roots! Let's try:
Solving Equations by Guessing
👀
Example
Solve all equations:
So far, we have been guessing solutions to equations. But guessing won't always work. Try guessing the roots of this beauty:
Not so simple anymore, right? To solve such and even more complex equations, we need a way to somehow simplify them, reduce them to obvious equalities…
Same Action Rule
We have defined what equalities and equations are. But inventing abstract objects just to do nothing with them later is absolutely useless. Objects are usually invented to perform actions on them later.
For example, let's take a true equality 6 + 3 = 9.
Let's depict it as scales:
Let's depict it as scales:
Let's perform some action with the left side of this equality. For example, add the number 2 to it. In the case of scales, this is equivalent to adding a weight of 2 to the left pan of the scales. The balance will be disturbed, and the scales will tilt to the left. The true equality 6 + 3 = 9 will turn into a false equality 6 + 3 + 2 = 9 or 11 = 9.
The equality became false because we performed the action only on one side — the left one. If we perform exactly the same action with the right side of the equality, add 2, then we will get a third equality, 6 + 3 + 2 = 9 + 2 or 11 = 11, and it is already true.
It turns out that it doesn't matter what we do with one part of a true equality. If we do the same thing with the other part, we will get a true equality again! Congratulations, we just discovered one of the most important and fundamental rules of mathematics!
Same Action Rule
If the same action is performed on both sides of a true equality (add, subtract, multiply, divide, or any other), the resulting new equality will also be true.
There is also a very simple formulation.
Remember it for the rest of your life:
Remember it for the rest of your life:
WHAT WE DID ON ONE SIDE, WE DO ON THE OTHER!
Proof. With ducks and communists!
True Preservation Examples
👀
Example
Try the same action rule for basic arithmetic operations:
What new equality will be obtained if, according to the same action rule, you add the number 2 to the equality below?
So why do we need this rule? What's the point of these useless examples? The point is that this rule allows us to transform any equality. For example, to reduce complex equalities to elementary ones without changing their truth! Started with a true one? Transform it a hundred times, in the end it will still be a true equality!
It turns out that with the help of this rule, one can easily and simply solve equations!
Elementary Equations
The overwhelming majority of all equations in mathematics (and in other sciences) are solved using the same action rule. This is the most fundamental, basic, and incredibly powerful tool in its simplicity.
Let's test it in action! Let's try to solve some simple equation, for example:
Recall that “solving an equation” means finding numbers that turn it into a true equality. We will assume “in advance” or “on credit” that the equation has solutions, and therefore we are working with a true equality. And since we are working with a true equality, we can apply the same action rule, obtaining from it new true equalities. Let's subtract the number 3 from both sides of the equation. According to the rule, from a true (by our assumption) equality we get a new true equality:
From the true equality x + 3 = 10, we obtained the true equality x = 7. Since the equality x = 7 is true, it means that x and 7 are one and the same, that is, the unknown number x is the number 7. And so we found the solution to the equation! We can even perform a check and substitute the number 7 instead of x in the original equation x + 3 = 10:
For clarity, let's represent the solution of this equation in the form of actions with scales. Unlike other examples, here on the left pan of the scales we have a weight with an unknown weight x. We remove a weight of 3 from the left pan, and on the right we “tear off” a piece of the same weight from a weight of 10. On the obtained new scales, we are essentially weighing a weight with an unknown weight x. And it “weighs” exactly 7:
Visualization of solving the equation x + 3 = 10
Simplifying to the Obvious
When starting to solve an equation, we assume it is a true equality from the start. This allows applying the same action rule time after time and obtaining simpler true equalities until it becomes obvious what the unknown is equal to.
The main question in solving equations is how many and what actions need to be performed to simplify the equation to an obvious equality. Now we will deal with this question using the example of the most elementary arithmetic operations: addition, subtraction, multiplication, and division.
Addition and Subtraction
With addition and subtraction, everything is quite simple. The main task is to add or subtract a number so that 0 is obtained. This way you can get rid of unnecessary and interfering pieces of equalities. Let's look at examples. Be sure to carefully study the solution of each, there are tricky nuances:
Multiplication and Division
In addition and subtraction, we simplified equalities by “eliminating” interfering pieces by reducing them to 0. With multiplication and division, there is a simeliminating“ interfering pieces by reducing them to 0. With multiplication and division, there is a similar simplification tool. Instead of ”eliminating“ through zero, for these operations reduction (or cancellation) is used to reduce interfering pieces to 1.
Equations with Multiplication and Division
😀
Elementary
Solve the equations using the same action rule:
By the way, those who are just learning to solve equations often have a desire to drastically simplify the equation by multiplying both sides by 0.
There is nothing wrong with this, and this action is not a mistake. Although we received a true equality, we lost absolutely all information about it, including information about the unknown variable! From 0 = 0 there is no way to get any more information about x. Therefore, such an action is absolutely useless.
Chains of Actions
All previous equations are elementary, and they can well be solved by trivial guessing. To solve them, we used only one action with both sides and can be solved by trivial guessing. To solve them, we used only one action with both sides of the equality. But no one forbids performing several actions one after another or even a whole chain of actions on the equation!
This is the strength's time to demonstrate this power with examples:
Many Ways — One Result
Almost always equations can be solved in several ways. Some can be solved quickly using advanced actions (exponentiation, taking roots, etc.), while others are more cumbersome but use elementary arithmetic operations.
Yes, even within the framework of elementary actions there are many different options:
One Equation — Different Solutions
😀
Elementary
Solve both equations from the problem above in other ways:
This time try to first subtract 4x from both sides of the equation.
There is no ”right“ or ”wrong“ way to solve equations. It is only important to always adhere to the same action rule and not forget that the action happens with the entire equality, and not just with one of its parts. And the skill to immediately recognize a short path will come with time and experience in solving a large number of equations.
Action is Always “Global”
When you decide to multiply, divide, add, subtract or do something else with a side of the equality, this action must be performed on the entire side as a whole, and not just on its individual elements. If you multiply or divide, then do it to the entire side, enclosing it in brackets. You cannot multiply/divide only by one fraction or only by one term!
Beginners regularly forget about this extremely important aspect of the same action rule when they want to quickly get rid of an inconvenient fraction or a complex expression. Let's analyze a typical mistake:
“Globality” Error
😀
Elementary
Look at the incorrect solution of the equation and think about where the mistake was made. Check yourself by looking at the correct solution and finding the root of this equation.
To avoid such mistakes, always remember that the action on the equation applies to its entire left and right part, and not to any separate elements.
Action is Always “Global”
When transforming equalities, always apply the action to the entire side of the equality as a whole as a single unit, and never to its individual parts!
Common Mistakes
We have covered all the key aspects related to solving elementary equations. Now be sure to pay attention to a number of misconceptions and mistakes that very often arise among beginners. Perhaps you yourself, without noticing it, also make some of the mistakes below.
- “Equation” is when “equals 0”A common misconception that arises because many practice equations in textbooks and problem books are written in the form . As you have already seen for yourself from the examples above, to the left and right of the equal sign there can be anything: numbers, variables, fractions and even complex expressions.
- “To solve an equation” means to find xComplete nonsense. Unfortunately, such an illiterate answer you will hear in 90% of cases from schoolchildren and even students. To start with, the variable is not always denoted by the letter x. A variable can be denoted by any letters and symbols, for example y, z, t, , etc.But generally, as soon as you hear such an answer, immediately poke your finger at x and confidently declare — “Find x? Well, here it is! That's it? Is the equation solved?”After you finish laughing, don't forget to tell what it actually means “to solve an equation”.
- Solving equations “in a line”Mathematical expressions can usually be transformed (performing cancellations, opening brackets, collecting like terms) in a single line via a chain of equalities. For example, simplifying the expression , we can write:Very often beginners try to apply exactly the same approach when solving equations. It looks different every time, but always incredibly creatively, for example:This is a natural mistake, but it must be nipped in the bud. Doing so is fundamentally wrong! Each new action on both sides, each “internal” transformation, everything must be on a separate line one under another:
- Confusion with equivalent transformationsRegularly after studying the rule of the same action on equations and equalities students start confusing it with ordinary expression transformations. Consider this example:on the left side the fraction can be safely cancelled by 4 and get 2x = 7. But students are afraid to do this, because if “if I cancel the fraction on the left, then according to the rule of same action I have to cancel on the right too”. And since on the right nothing cancels with anything, it means you can't do that.Here you just need to understand that cancelling a fraction is essentially just replacing one notation, , with another, 2. Both these notations denote the same number, and therefore they can be freely replaced with each other. Such actions are also called equivalent transformations — the form changes, the value does not. In analogy with mechanical scales this can be compared to removing a weight of 3 kilograms and instead of it putting a bucket of water weighing 3 kilograms — it looks different, the essence is the same.Never confuse equivalent transformations (cancelling fractions, opening brackets, collecting like terms, etc.), which do not change the essence in any way, with the same action rule, which completely changes the equation! With equivalent transformations no actions are required for “compensation” — there is simply nothing to compensate!
The Mystery of “Flying” Numbers
Unfortunately, the vast majority of schoolchildren and students are not familiar with the concept of equality as ”scales“ and the rule of the same action that intuitively follows from itales” and the intuitively following from it rule of the same action. Therefore, they solve equations according to a whole set of rote-learned rules: numbers with plus and minus fly across the equal sign with the opposite sign; fractions on different sides of the equality are aligned by the method of “cross multiplication” and other mystical stories straight from the pages of the magazine “Mysteries of the 20th Century”.

sking them to explain the essence of the actions performed almost always results in surprised blinkinguest to explain the essence of the actions performed almost always causes only surprised blinking of eyes… “well, that's just the rule” — that's the only answer they can give. Remember once and for all:
NUMBERS ARE NOT MIGRATORY BIRDS! THEY CANNOT FLY!
Compare two approaches when solving the equation x – 5 = 8:
- 1We dance with a tambourine, jump over a fire three times and move –5 to the right with the opposite sign. We get x = 8 + 5. The answer is 13. And why and how it happened, don't even think…
- 2The number –5 prevents x from being alone. We need to get rid of it. To do this, add 5 to the left part of the equality. –5 and 5 sum up to 0, and x remains alone: . By adding 5 on the left, we disturbed the balance. Having done something with one part of the equality, the same action must be performed with the other, then it will preserve its truth. Therefore, add 5 on the right too: x = 8 + 5. The answer is 13.
The first option is shorter. And that is its only plus. But if the ritual is forgotten, it is impossible to restore it, because there is no understanding of why certain actions are performed. Rote-learned rituals are also impossible to adapt to other situations, because the logic that gave birth to these rituals is not clear.
The second option uses a universal and intuitively understandable rule. Each step is logical and justified. Once you understand — and you remember the essence/idea forever. It is not necessary to explain it so in detail every time in words.
Never use rituals in mathematics. They are flawed and do not develop you in any way. There is nothing worse than mindlessly memorizing “ready-made algorithms” instead of fully understanding the actions performed.
Why Solve Equations?
Equalities and equations are literally everywhere! Countless real-life situations can be reduced to equations, that is, literally translated into the language of mathematics. Therefore, transforming equalities and solving equations is a basic and key skill not only in mathematics, but also in any exact science. Confident mastery of this skill is like a reliable and universal workbench for working with thoughts and ideas.
The Idiot's Triangle
The most glaring, illustrative and funny example of the inability to work with equalities and equations, when memorization is prioritized over understanding, is the so-called “magic triangles of formulas” for “simple” memorization of formulas in physics and even mathematics!

Epidemic of magic triangles
Such triangles work very simply — you cover the letter you want to find with your finger, and from the remaining letters you get a ready-made formula. If the letters are on the same level, they are multiplied, if on different ones — divided:
And what is funny about this? On the contrary, it is quite witty! It is indeed invented wittily, and looks beautiful, but there is exactly zero sense. Possessing the most elementary skills of working with equalities, no magic triangles are needed at all!
It is enough to understand and remember at least one version of the formula. In the case of speed, it is easiest to understand that speed is distance “broken down” by time segments, that is, distance divided by time:
That's all you need to know. And if the problem asks to find the distance? It means that in the equality above we need S to remain alone. By the rule of the same action multiply both sides of the equality by t. Then on the right side t and t will cancel (t : t = 1), and only S will remain there:
There you go, in 10 seconds from the speed formula we obtained the distance formula. Time is found through speed in a similar way. Without any magic triangles and other nonsense!
Just like that, knowing only one basic formula, you don't need to memorize anything else, because you can always obtain all other formulas you need by elementary actions on equalities. This applies not only to speed, but also to all other formulas in physics and mathematics. Learn to understand the essence, not to memorize beautiful pictures!
Equations in Life
One of the equations' superpowers is that they allow us to translate questions arising in real life onto “mathematical rails”.
We take a daily situation, identify numerical values in it, denote what we are looking for with variables, and set up equations. And once we manage to write down the problem in the form of an equation, we can use the rules and methods described above to solve it. Here is a clear demonstration:
Applying equations in life
Applied
😀
Elementary
No matter what sphere of human activity you take, you can find equations everywhere!
Alina wants to buy a new phone, which currently costs 10,000 rubles. Every day she saves 100 rubles. However, every day the price of the phone increases by 20 rubles! How many days does she need to save money to accumulate the necessary amount?
In fact, examples of applying equations in real life are endless. The examples above are only the most elementary, but still useful situations. That is why it is so important to be able to solve equations!
Actions can be anything
We considered only the most elementary actions on equalities and equations: addition, subtraction, multiplication, and division. But in mathematics there is a huge variety of other actions:
- Exponentiation
- Root extraction
- Taking logarithm
- Taking absolute value
- and so on…
And for all of them, naturally, the rule of the same action works!
Not only numbers and letters can participate in equalities, but also entire functions. Then they can be, for example, differentiated or their limits found:
The objects and actions themselves become more and more abstract. In higher mathematics you will encounter matrices, non-geometric vectors, operators, functionals, and so on… Convenient analogies with scales will lose all meaning, but the rule of the same action will still work perfectly! This is one of the most universal principles of mathematics, which operates at all its levels.